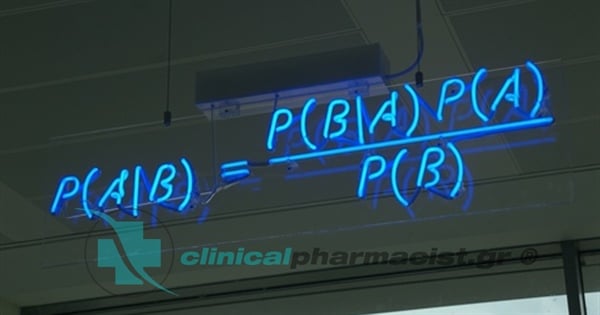Θα ήθελα να σας ζητήσω μια χάρη. Πριν διαβάσετε τη συνέχεια του άρθρου παρακάτω, σας παρακαλώ πολύ να απαντήσετε αυθόρμητα στις ερωτήσεις που ακολουθούν, ψηφίζοντας την καλύτερη, κατά τη γνώμη σας, επιλογή: 

Όπως έχουμε αναφέρει και παλιότερα, είναι γεγονός ότι ο ανθρώπινος εγκέφαλος δεν τα πάει και πολύ καλά με τους αριθμούς. Ιδιαίτερα δε, δεν τα πάει καλά με τα ποσοστά και τις πιθανότητες: Απλούστατα, δεν είμαστε σχεδιασμένοι να αντιλαμβανόμαστε ενστικτωδώς τις πιθανότητες βάσει των κανόνων της στατιστικής. Μπορείτε να διαβάσετε αναλυτικά τους λόγους για τους οποίους συμβαίνει αυτό στο, μικρό αλλά εξαιρετικό, blog «What the stats!?!»· περιληπτικά, ισχύουν τα εξής:

• Έχουμε την εγγενή τάση να βγάζουμε βιαστικά συμπεράσματα.
• Υπερεκτιμούμε το επίπεδο των γνώσεών μας.
• Ανακαλύπτουμε μοτίβα εν μέσω τυχαίων δεδομένων.
• Δεν αντιλαμβανόμαστε ότι συμπτώσεις συμβαίνουν συνέχεια.
• Αντιλαμβανόμαστε ενστικτωδώς τις πιθανότητες με λάθος τρόπο.
• Δυσκολευόμαστε με τους συνδυασμούς πιθανοτήτων
• Δεν έχουμε τη δυνατότητα να κάνουμε υπολογισμούς Μπαεσιανών πιθανοτήτων ενστικτωδώς.
• Έχουμε την τάση να αγνοούμε πιθανές εναλλακτικές εξηγήσεις, ιδίως όταν έρχονται σε αντίθεση με την προσχηματισμένη γνώμη μας. 
• Πέφτουμε θύματα ενός φαινομένου που είναι γνωστό ως «πλάνη της παλινδρόμησης».

Έχοντας στο νου μας τα παραπάνω, ας δούμε προσεκτικά τα δύο ερωτήματα της πρώτης παραγράφου.

HIV SCREENING

Το τεστ για τον ιό HIV με τα συγκεκριμένα χαρακτηριστικά ευαισθησίας και ειδικότητας είναι υπαρκτό, και μάλιστα ένα από τα καλύτερα της αγοράς, σύμφωνα τουλάχιστον με την παρουσίαση του FDA από όπου και αλίευσα τα στοιχεία του, αν και δεν έχει ιδιαίτερη σημασία αυτό ως προς τον σκοπό του παραδείγματός μας. Ευαισθησία (sensitivity) είναι η ικανότητα ενός διαγνωστικού τεστ να βγάζει ορθό θετικό αποτέλεσμα. Δηλαδή, στην περίπτωσή μας, το 99,9% σημαίνει ότι, αν κάνουν το τεστ 1000 φορείς του HIV, αυτό θα βγάλει θετικό αποτέλεσμα για τους 999.  Ειδικότητα (specificity) είναι η ικανότητα του τεστ να βγάζει ορθό αρνητικό αποτέλεσμα. Δηλαδή, αν χίλιοι υγιείς άνθρωποι κάνουν το τεστ, οι 991 θα βγουν αρνητικοί για την ύπαρξη του ιού, αλλά υπάρχουν και 9 που θα λάβουν ψευδώς θετικό αποτέλεσμα.

Τι θα συμβεί λοιπόν αν χρησιμοποιήσουμε αυτό το τεστ για screening, δηλαδή προσυμπτωματικό έλεγχο, του γενικού πληθυσμού; Οι περισσότεροι θα υποθέσετε διαισθητικά ότι, για κάθε έναν που θα βγαίνει θετικός στο τεστ, θα ισχύει πως κατά 99,9% είναι φορέας του HIV -λογικό ακούγεται. Όμως, οι πιθανότητες κατά Bayes ορίζουν πως ο υπολογισμός πρέπει να γίνεται «υπό όρους», έχοντας γνώση των προϋποθέσεων που ισχύουν. Οι προϋποθέσεις στο παράδειγμά μας είναι ότι, A: Κάποιος έχει τον ιό Β: Κάποιος βγαίνει θετικός στο τεστ.

Σύμφωνα με το θεώρημα Bayes, η πιθανότητα P(A|B) κάποιος που λαμβάνει θετικό αποτέλεσμα να είναι και φορέας του ιού, υπολογίζεται από τον τύπο P(A|B)=P(B|A)xP(A)/P(B), όπου P(B|A) είναι η πιθανότητα κάποιος που έχει τον ιό να βγει θετικός και P(A), P(B) οι ανεξάρτητες πιθανότητες των ενδεχομένων Α και Β. Ας τα υπολογίσουμε: Η πιθανότητα P(B|A) είναι η ευαισθησία του διαγνωστικού τεστ και η P(A) o επιπολασμός της νόσου, η συχνότητα εμφάνισης δηλαδή του HIV στον γενικό πληθυσμό. Για την Ελλάδα, σύμφωνα με αυτή την πηγή, το ποσοστό στους ενήλικες είναι 0,2%, άρα ο αριθμητής του κλάσματος γίνεται P(Β|Α)xP(A)=0,999×0,002=0,001998. Η πιθανότητα κάποιος να βγει θετικός στο τεστ, ανεξάρτητα αν έχει τον ιό ή όχι, είναι το άθροισμα τoυ γινομένου P(B|A)xP(A) που υπολογίσαμε προηγουμένως, και της πιθανότητας κάποιος που δεν έχει τη νόσο να λάβει θετικό αποτέλεσμα, δηλαδή 0,998×0,009=0,008982. ‘Aρα P(B) = 0,001998 + 0,008982=0,01098 και, υποκαθιστώντας στον γενικό τύπο, προκύπτει ότι P(A|B) =  0,1819 ή 18.2%.

Σωστά διαβάσατε.

Το αποτέλεσμα αυτό σημαίνει το εξής: Αν το παραπάνω τεστ εφαρμοστεί για τον προσυμπτωματικό έλεγχο του ιού του AIDS στον γενικό πληθυσμό της Ελλάδας, κάθε θετικό αποτέλεσμα θα έχει μόλις 18,2% πιθανότητα να είναι αληθές. Πράγμα που σημαίνει με τη σειρά του, ότι είναι προτιμότερο στατιστικά να το παίξει κανείς κορώνα-γράμματα! (50%).

Δικαίως θα μας πείτε τώρα, μα καλά, είναι δυνατόν να είναι τόσο άχρηστο ένα διαγνωστικό τεστ με 99,9% ευαισθησία και 99,1% ειδικότητα; Η απάντηση είναι: εξαρτάται από τον τρόπο χρήσης του. Ένα τέτοιο τεστ είναι άχρηστο για το γενικό screening του πληθυσμού, ειδικά όταν η πραγματική επίπτωση της νόσου είναι τόσο μικρή στο σύνολο. Υπό διαφορετικούς όρους όμως, όταν αφορά υποσύνολα ανθρώπων που εμφανίζουν σημαντικά μεγαλύτερη επίπτωση (π.χ., χρήστες ενδοφλέβιων ναρκωτικών, ομοφυλόφιλοι άνδρες κ.ο.κ), η διαγνωστική του αξία αυξάνεται. Ακόμα και σ’ αυτές τις περιπτώσεις όμως, η πραγματική του αξία βρίσκεται στο αρνητικό αποτέλεσμα, το οποίο είναι αληθές στο 100% των περιπτώσεων.

Αυτός ο αριθμός στον οποίο καταλήξαμε, το 18,2%, ονομάζεται θετική προγνωστική αξία και αυτό είναι τελικά το μέγεθος που μας αφορά ως «αρρώστους» αλλά και ως «γιατρούς», όχι η ευαισθησία και η ειδικότητα, που είναι μεγέθη που αφορούν το ίδιο το τεστ και έχουν νόημα μόνο εντός συγκεκριμένου πλαισίου.

Μπορείτε να πειραματιστείτε με τους αριθμούς χωρίς να κάνετε υπολογισμούς με το χέρι, υπολογίζοντας την προγνωστική αξία πραγματικών (ή φανταστικών) μεθόδων με βάση την ειδικότητα, την ευαισθησία και το ποσοστό του πληθυσμού που αφορά η νόσος στην ιστοσελίδα http://www.medcalc.com/bayes.html.

ΕΜΒΟΛΙΑΣΤΙΚΗ ΚΑΛΥΨΗ

Συνεχίζοντας τους πειραματισμούς μας με τους αριθμούς, ερχόμαστε σε ένα αγαπημένο θέμα της ιστοσελίδας. Για την ακρίβεια, η ιδέα για το ίδιο το άρθρο ξεκίνησε από μια συζήτηση μεταξύ επιστημόνων υγείας, με αφορμή την σχετική ερώτηση που βρίσκεται στην αρχή.

Η αυθόρμητη απάντηση συνήθως είναι κάτι σαν «90%; Δεν είναι κι άσχημα».

Αν εξετάσουμε το θέμα από την πλευρά της επιδημιολογίας των λοιμωδών νόσων, τα πράγματα, δυστυχώς, είναι αρκετά διαφορετικά.

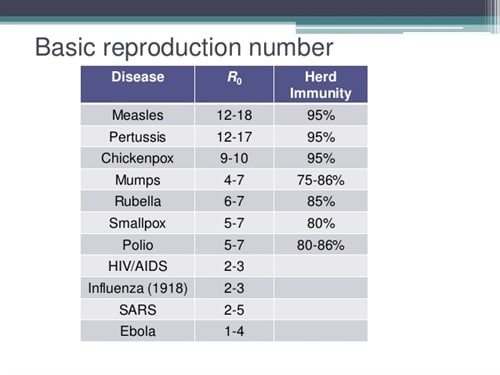
Βασικός παράγοντας που πρέπει να γνωρίζουμε πριν αποφανθούμε, είναι η μεταδοτικότητα της νόσου. Εκφράζεται με το μέγεθος R₀, που λέγεται βασικός αριθμός αναπαραγωγής, υπολογίζεται μαθηματικά, και αποτελεί τον αριθμό των ατόμων που θα μολύνει ένας ήδη μολυσμένος άνθρωπος, όταν εισέλθει σε πληθυσμό που αποτελείται από 100% ευαίσθητα άτομα. Για τον ιό της ιλαράς το R₀ έχει υπολογιστεί σε 12-18 (συνηθέστερα συναντάται το 18).

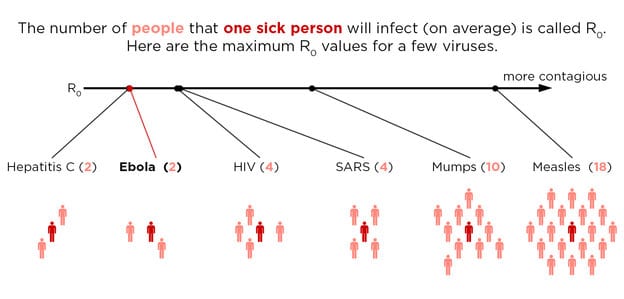
Από το R₀ προκύπτει και το λεγόμενο «Herd Immunity Threshold», δηλαδή το ελάχιστο όριο ατόμων με ανοσία σε έναν πληθυσμό, έτσι ώστε αυτά να δρουν προστατευτικά, σχηματίζοντας έναν «τοίχο» μέσω του φαινομένου που ονομάζεται ανοσία του κοπαδιού, περιορίζοντας τα ξεσπάσματα επιδημιών μεταξύ αυτών που δεν έχουν ανοσία (μη εμβολιασμένοι ή σε ανοσοκαταστολή). Ορίζεται ως 1-1/R₀ και για την ιλαρά βγαίνει 0,944, δηλαδή το κατώφλι για να επιτευχθεί ανοσία της κοινότητας είναι 94,4%. Το ποσοστό αυτό αφορά την πραγματική ανοσία, όχι το ποσοστό του εμβολιασμού. Λαμβάνοντας υπόψη πως,

1. για άγνωστους λόγους, περίπου το 1% των εμβολιασμένων ατόμων δεν αποκτά ανοσία,
2. τα μικρά παιδιά κάτω των 15 μηνών δεν εμβολιάζονται για τον ιό της ιλαράς,
3. σε ορισμένες παθήσεις αντενδείκνυται ο εμβολιασμός και
4. ένα ποσοστό του πληθυσμού βρίσκεται σε ανοσοκαταστολή (καρκινοπαθείς, ασθενείς με AIDS, μεταμοσχευμένοι κ.ο.κ.),

ο στόχος για το ποσοστό του εμβολιασμού πρέπει να είναι πολύ πάνω από αυτό το όριο και να πλησιάζει το 100%.

Ίσως σας φαίνεται υπερβολικό να διαβάζετε ότι καταρρέει η ανοσία σε μια κοινότητα με εμβολιαστική κάλυψη 90%. Όπως και προηγουμένως, θα επιστρατεύσουμε τα μαθηματικά για να σας αλλάξουμε τη γνώμη.

Ο πραγματικός αριθμός αναπαραγωγής (effective reproduction number), R ή R(e), προκύπτει αν πολλαπλασιάσουμε το R₀ με το κλάσμα του πληθυσμού που είναι επιρρεπές σε λοίμωξη. Αν το R < 1, τότε η επιδημία φθίνει και τα περιστατικά μειώνονται. Αν το R = 1, ο αριθμός των περιστατικών παραμένει σταθερός, δεν έχουμε ξέσπασμα δηλαδή. Αν R > 1, τότε τα περιστατικά αυξάνονται εκθετικά. Υποκαθιστώντας τα νούμερα για την περίπτωση του 90%, έχουμε R= 18×0,1 = 1,8. Δηλαδή σε μία κοινότητα με ποσοστό εμβολιαστικής κάλυψης 90%, η εμφάνιση ενός άρρωστου με ιλαρά θα οδηγήσει σε εξάπλωση της ασθένειας μεταξύ των επιρρεπών μελών της κοινότητας με εκθετικό ρυθμό, όπου κάθε ένας που θα μολύνεται θα την μεταδίδει σε άλλους δύο περίπου, οδηγώντας στην κατάρρευση της ανοσίας του κοπαδιού.

Στα παρακάτω βίντεο, μπορείτε να παρακολουθήσετε την προσομοίωση μιας επιδημίας ιλαράς στην πόλη της Νέας Υόρκης με ποσοστό εμβολιαστικής κάλυψης 80% και αντίστοιχα με ποσοστό 95%. Στην περίπτωση του 90%, αυτό που θα άλλαζε θα ήταν ο χρόνος εμφάνισης της απότομης αύξησης των περιστατικών, όμως η τελική εικόνα, αν και σαφώς βελτιωμένη, θα έμοιαζε πάρα πολύ με αυτήν του 80%.

Οι προσομοιώσεις δημιουργήθηκαν με τον FRED Measles Epidemic Simulator του University of Pittsburgh, διαθέσιμο στη διεύθυνση http://fred.publichealth.pitt.edu/measles/.

Κλείνοντας, θα ήθελα να επισημάνω κάτι που προκύπτει από τους αριθμούς για την ιλαρά. Δυστυχώς, το μεγάλο R₀ σε συνδυασμό με άλλους παράγοντες, όπως η μόνιμη ύπαρξη δεξαμενής ευαίσθητου στην ιλαρά πληθυσμού (παιδιά κάτω των 15 μηνών) σημαίνει πρακτικά ότι η εξάλειψη της νόσου είναι σχεδόν αδύνατη, τουλάχιστον μόνο μέσω των εμβολιασμών. Αυτό εφιστά ακόμα πιο επιτακτική την ανάγκη διατήρησης της ανοσίας του κοπαδιού στην βέλτιστη κατάσταση και της επιθετικής, κατά τη γνώμη μου, αντιμετώπισης φαινομένων λειτουργικού αναλφαβητισμού και τσαρλατανισμού που κρύβονται πίσω από τη μόδα του αντιεμβολιαστικού κινήματος.

  Ημερομηνία τελευταίας αναθεώρησης: 10/5/2022

Μοιραστείτε τη γνώση!